Noviembre

Integración en el plano complejo

Para la realización de ejercicios en el plano complejo se debe considerara varios aspectos ya que no se procede de la misma manera que con funciones reales ya que la función para ser integrada debe cumplir que :

• Sea continua en el dominio en la cual se desea integrar la función.
• La derivada de la curva en la cual se desea integrar la función sea diferente de cero (sea una curva suave).

 Esto se lo considera debido a que  los números complejos se los puede representar en el plano complejo (Plano de Gauss) con lo que se las puede considerar como integrales de linea .

Aplican las mismas propiedades que en las funciones reales

Integrales cerradas

La parte mas importante de la utilización de las integrales cerradas es el uso de el Teorema  de Cauchy que  nos permiten simplificar el calculo debido a que si al cumplir  ciertas condiciones el valor de la integral es cero.

• Condiciones:

1. La función sea analítica 
2. El dominio sea simplemente conexo
3. Y la curva sea cerrada simple.

Integrales indefinidas

Si f(z) tienen anti derivada (integral), se puede calcualar la integral indefinida como F´(z)=f(z), entonces:

Curvas en el plano complejo

Son de suma importancia debido  que nos permiten los valores de las integrales por lo que s importante saber las maneras mas rápidas para su parametrizacion como medida mas conveniente y practica para la resolución de ejercicios.

Parametrizacion de algunas curvas suaves:

Dominio simplemente conexo.

Condiciones:

• Si solamente contienen puntos en su dominio
• Si no presenta agujeros en su dominio.

Curva simple ( curva de Jordan)

Es una curva simple si no presenta entrecruzamientos o puntos dobles.

Independencia de la trayectoria

Relevante debido a que es una forma muy simplificada para realizar integrales para lo cual debe cumplir que :

• La curva sea analítica en D 
• Tenga un dominio simplemente conexo

Entonces la integral es independiente de la trayectoria en la que se analice por lo que se le puede aplicar la ecuación de Cauchy para calcularla , eligiendo un dominio o curva al azar generalmente se escogen circunferencias para la simplificación de cálculos.

Tomando como positivo el sentido anti horario de cualquier función.

Integrales Cerradas

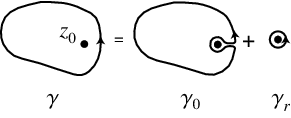
Teorema de Integral de Cauchy

Teorema de la deformación

Fórmula de la Integral de Cauchy

Sucesiones y series de variable compleja.

Son similares a las sucesiones y series de variable real. Para determinar la convergencia se los utiliza los mismos criterios.

• Series de Taylor propia de números complejos.
• Series de Caurent analizar convergencia tanto en números reales como complejos.

Sucesiones.

Es una función de naturales en los complejos con una cantidad infinita de elementos

• Propiedades.

Series.

Son la suma de los elementos de una sucesión y su convergencia se lo realiza con los criterios de series reales.

De este criterio podemos sacar que si el sumatorio de zn=0 la serie converge en caso contrario diverge.

Series especiales.

Serie armónica

Diverge siempre.

Serie "p"

Criterios de convergencia

Series de Potencia.

 De esta manera podemos calcular la convergencia de la seria la cual se dará por intervalos calculando su radio de convergencia de la siguiente manera:

Bibliografía:

• http://netlizama.usach.cl/Apuntes%20Variable%20Compleja.pdf
• http://cb.mty.itesm.mx/ma3002/materiales/ma3002-series-fourier.pdf
• http://gaussianos.com/convergencia-de-sucesion-de-numeros-complejos/
• http://slideplayer.es/slide/1018370/