Octubre

Los Números Complejos

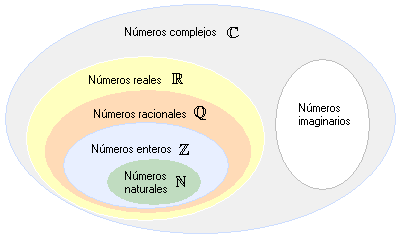
Del gráfico podemos deducir lo siguiente:

• Todo numero real es un complejo.
• No todo numero complejo es un real.

Los números complejos se los representara de la siguiente forma:

Z=x+iy

 de donde

Re(z)=x         "Parte real"

Im(z)=y         "Parte imaginaria"

x,y elemento de los reales.

Representación cartesiana.

Igualdad entre números complejos.

Si Z1=x1+iy1 y Z2=x2+iy2

Z1=Z2 si solo si

x1=x2 y yi=y2

Casos particulares:

1. Si Re(z)=0 y Im(z)=0 entonces Z=o+0i (cero complejo)
2. Si Re(z)=0 y Im(z) diferente a 0 entonces z=yi (imaginario puro)
3. Si Re(z) diferente de 0 y Im(z)=0 entonces z=x (Numero real)

Operaciones con números complejos

Producto:



Como se puede observar en el ejemplo en la multiplicación de números complejos se multiplica como se fueran dos binomios  multiplicando los dos términos de cada uno.

Un conocimiento necerario para facilitar la obtención de valores en la multiplicación es saber que existen potencias de i que van en series de 4 como se vera en la siguiente gráfica.

• Conjugado de z

Sea z=x+iy entonces su conjugada es z(conjugado)= x-iy

• Modulo de z

Se la calcula de la misma forma que el modulo de un vector.

Propiedades  del conjugado y del modulo de un complejo.

Forma polar de un numero complejo.

Teorema de Euler:

Para la mejor apreciaron de teorema consideraremos a los números complejos como vectores con coordenada x,y de los cuales podemos transformar de coordenada rectangulares a polares de la siguiente manera o con la utilización del su angulo.

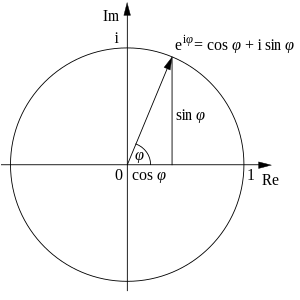
Entonces:

Al tratar de elevar a una potencia un numero complejo en vez de  de elevarlo al mismo utilizando factoreo considerándolo como un binomio elevándolo a la"n" potencia se puede trabajar como si el complejo propuesto fuere un exponencial.

Este concepto es explicado por el denominado teorema de Euler.

El mismo que nos facilita las operaciones de potencia y la obtención de raíces en los números complejos.

Potencia:

Trabajando con la forma polar del complejo se tiene que:

Raíces:
Trabajando con la forma polar del complejo se tiene que:

Donde k varia de 0 a n-1

De esta forma podemos concluir que de una raíz cubica se sacaran 3 resultados en los complejos , lo mismo para con una raíz cuarta 4 resultados y así sucesivamente.

Lugares Geométricos en C

Existen varias formas de representar gráficamente a las funciones complejas las mas comunes son:

• Distancia

• Circulo

• Rectas

Funciones complejas

Para la realización de gráficas en C se tomara una nueva forma de expresar a un numero complejo:

w=u(x,y)+iv(x,y) de esta forma necesitaremos 4 planos para graficar una función lo cual es imposible de esta forma aremos uso de un artificio matemático para transformar de los planos Re () e Im() a los planos de u y v de los cuales podremos estudiar ciertas propiedades.

Representaciones gráficas

Transformaciones del plano complejo.

Limites

Continuidad

Derivación 

Ecuaciones de Cauchy -Rieman (E.C.R)

• Coordenadas conjugadas

• Funciones analiticas

Funciones Armónicas

Funciones Trascendentes básicas(fundamentales)

Bibliografía:

• http://www.academica.mx/sites/default/files/adjuntos/136985/complejosteorico.pdf
• http://ocw.unican.es/ensenanzas-tecnicas/fundamentos-matematicos-i/fundamentosmatematicosi/ejercicios-resueltos/Bloque1_NumerosComplejos.pdf
• http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C02_Funciones_complejas.pdf
• http://corcoles.org/uoc/anmat/es/es32.xml